How To Learn Maths

I suppose the TL;DR version here would be “I don’t really know”, but I’m going to try to outline some of my thinking on this based on some of my experiences teaching classes at a university and my musings over the years, which are far less ‘evidence-based’ you could say.

Motivation

The first thing that strikes me is that it’s very hard, extremely hard, to get anyone to learn anything if they don’t have the motivation to do so. Motivation, unlike sex, exists on a spectrum and there are, broadly speaking, two kinds of motivating factors; the positive and the negative. A positive motivating factor would an interest in the subject matter, a negative motivation would be grades. Both motivate the student to learn, but one is supportive and the other not so much. I suppose one might say it’s the difference between forced labour and doing something as a hobby.

If you’re positively motivated (and you will almost certainly also be motivated by grades) it doesn’t feel like so much work and your brain goes about it with some relish. If you’re only negatively motivated then you’re in a constant struggle with your brain which is telling you “this is so boring, why am I doing this, please make it stop”.

Obviously, as an ‘educator’ or just your plain and mundane common garden-variety teacher, you’re going to want to improve the degree of positive motivation. It makes life easier for the students and also makes your job much easier. If it’s all just about grades you become the enemy, in a way. You’re the bastard that’s stopping them from getting the A that they want and feel they deserve.

This is why so much effort has been expended over the years to make maths ‘exciting’ and ‘relevant’ in the vague hope that this improves the degree of positive motivation. It’s not entirely a futile hope, but it comes at a price if you forget the most important element.

The Taj Mahal is often said to be one of the world’s most beautiful buildings, but I can guarantee you that the workers laying the foundations weren’t looking at their handiwork and saying “cor blimey, will you look at the foundations on that!”. The finished product may look spectacular, but there were a lot of tedious bits, not to mention hard work, that got you there.

Our brains are doing a kind of intuitive math all the time. If that function stops working we’d fall down the stairs everyday. We’re continually evaluating distances and movement and where to place our feet - and it all happens subconsciously. If we wanted to do a conscious analysis we’d have to get out the pen and paper and translate everything into that dreaded borefest of squiggly symbols and the like.

Our brains aren’t doing that, obviously, but some kind of lightning-fast equivalent process.

It’s not that we can’t ‘do’ maths, it’s that we can’t (often) do this kind of ‘conscious’ maths.

Making maths ‘exciting’, without also recognizing the work that is involved, is a bit like trying to get everyone to build a Taj Mahal without learning how to lay a foundation, or do the plastering.

Ideally, what you’re trying to do is to inculcate an attitude something like “Wow, that’s one seriously cool building. How can I learn the techniques so that I can make something like that one day?”

The thing is, and there’s no better way to express this, is that learning maths requires practice and work and this is, quite often, fucking boring. The key is to motivate the students to want to put in that work, the hours of practice that are required.

When I was learning to play the piano I did not like practicing scales and arpeggios and the like, but I recognised the foundational importance in learning technique and harmony that these things brought me. So, because I wanted to be able to play something a bit more than Chopsticks I dutifully put in the (very tedious) grind to learn the scales and to play them perfectly.

Actually, that’s not entirely true, either. For many years I was an indifferent student of the piano. It was only when I wrote my first song (it was bad) did my motivation suddenly take off. Instead of grudgingly doing half an hour’s practice a day, I was spending hours a day. My technique and capabilities improved beyond all recognition. My ability to improvise went from essentially zero to substantial.

Making maths seem exciting (and relevant), an approach I very much agree with incidentally, is part and parcel of trying to develop that “I want to work” attitude - but you still need to do the work if you want to develop any kind of mathematical facility.

The thing I’ve seen with some (over-optimistic) approaches to maths, which are much more fun and ‘intuitive’ than the way I learned, to be sure, is that the necessary ‘hard-work’ component gets shoved to the wayside.

Takeaway : the key is to motivate students to want to put in the (necessary) work

How : no idea, really. Yes, make things ‘exciting’ and ‘relevant’, which definitely helps a lot, but it isn’t quite the magic bullet that many seem to think it is¹.

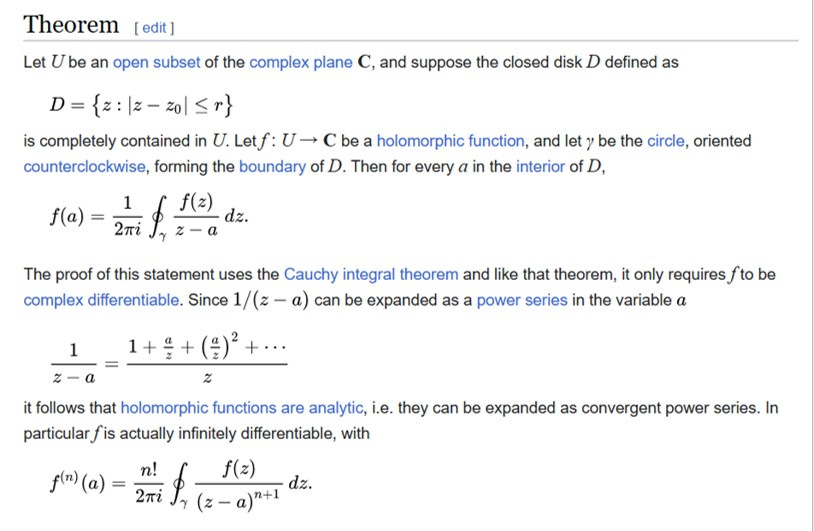
Some Serious Squiggles

OK - they certainly look pretty serious to your average person, but they’re actually 200 years old. This formula will (likely) be introduced during your first Complex Analysis course at university. Here it is (screenshot from Wiki which is, in general, pretty good for maths and physics stuff) :

Yikes. That’s a bit different to all the (mostly asinine) discussions we saw surrounding 2+2 = 5 during peak woke and all of the impossibly stupid ‘discussions’ some had about how maths was ‘racist’ or ‘white supremacist’ or promoted ‘whiteness’ or some other such cretinous drivel.

This is (200-year old) maths raw and in all its glory. And it’s fucking beautiful. I’m looking at this as I would the paintings on the roof of the Sistine Chapel, or feeling like I’m listening to the 2nd movement of Beethoven’s 7th symphony, or looking at the Taj Mahal.

When most internet discussions about ‘maths’ erupt these days they’re talking about the 2+2 = 4 level of maths - but things like Cauchy’s integral formula (the above theorem) are the kind of things this leads to (eventually).

But how am I to convince anyone that it is, as I suggest, fucking beautiful - almost indescribably beautiful? Perhaps I’m just some kind of pervert with a maths paraphilia.

How might I persuade the student that it’s really worth their time putting the effort in to really, properly, understand this thing, to motivate them?

The content of this theorem is amazing. Let’s imagine I took a walk round the perimeter of the Lake District in the UK (or Yellowstone in the US, for example). What this theorem means in these terms is that I would be able to know what’s ‘going on’ at any specified point within the park simply by walking round the boundary.

I find that extraordinary. Yet when I tried this sort of thing in class - to explain in ‘plain language’ the content of theorems - I was often met with the dreaded thousand yard stare.

I don’t think it’s all down to me. I tend to get quite passionate and animated and enthusiastic when talking about this kind of thing - so I don’t think I could be accused of ‘droning on’ like some robot. My maths ‘oratory’ could always be improved, of course, but I don’t think I was particularly bad it.

The only thing that reliably worked was “if you don’t know this, and know how to use it, you won’t get an A”.

Tracing the story of complex numbers from their origins in the 16th century (Cardano, 1545) through to Cauchy’s beautiful theorems, nearly 300 years later, is fascinating in itself. Complex numbers arose from trying to solve cubic equations in algebra, but they are generally introduced, today, by thinking about solutions to x² = - 1. The solution we’re looking for here is a number that when squared (multiplied by itself) gives the result - 1. That number is usually today given the symbol i.

There was, as you might imagine, a good deal of grumbling about this at the time with many describing it as a bit mad. We’ve ended up with the convention that numbers incorporating this thing i are known as complex numbers with a ‘real’ part and an ‘imaginary’ part - which I’ve always thought of as somewhat unfortunate. There’s nothing more ‘imaginary’ about multiples of i than there is with multiples of, say, 2².

The ‘real’ numbers sit within, and are a subset of, this much wider class of numbers, the complex numbers. All sorts of things become much clearer, in fact, when we extend our conception of ‘number’ in this way.

The history of ‘maths’ - or at least some of it - has been one of gradual extension of this concept of number. We learn to count, because it’s probably a good idea to know if someone’s nicked one of the cows in your field overnight. Then you get negative numbers; I owe you 2 cows becomes - 2.

Fractions become important when you want to butcher the cow - here’s your half of the cow.

Prime numbers become important when you have 17 cows and 3 sons and you want to leave them to your sons as their inheritance.

It all starts with number.

The First Steps

One way to introduce some maths to kids, and it also has the added benefit of really pissing them off, would be to start with a Mars Bar and say you’re going to share it with them. Cut off a small piece for them and keep the bigger piece for yourself³. Chances are your kid’s gonna recognize this as being unfair.

There’s already that chocolate nugget of ‘equality’ simmering away in their brain - you don’t really need to ‘teach’ them that. There’s already this concept of “this is bigger than that” - which, when you boil it down to its fundamentals, is a mathematical idea.

I’m not a mathematician, as such, although I love maths and so I can only hypothesise somewhat weakly that the physical structures like ‘this is bigger than that’ and ‘this sabre-toothed tiger is closer to you than me, which is fantastic’ imply a particular kind of maths appropriate for the description of the physical world. It’s a world with an ordering (closer/further) and a metric.

But most parents, I think, do introduce ‘number’ to kids from very early on. They’ll maybe count out toast fingers as they’re putting them on a plate, or count the number of blocks they stack to make a tower (before the little Godzilla brings it crashing down).

There’s loads of ways to introduce number and addition and subtraction to kids during play and doing it in a natural way that is part of a game. This is something I would greatly encourage - but don’t force it. It should always be light and fun and part of the game. Remember to stop when they lose interest.

You can even introduce division early on through a game. You might, for example, sit down with Alice, Bob, and Carol - three of their favourite soft toys - and take 6 sweets (candies) and give 3 to Alice, 2 to Bob, and 1 to Carol. Hopefully, your kid will be able to see this is unfair. You can pretend to be Carol crying, or Alice smiling and get your little one to figure out how to make everyone happy by sharing the sweets out equally. They’ll get the idea that for some amount of sweets you can achieve this ‘fair’ division.

You probably don’t want to overdo this lest you train the next generation of Communists, though.

What you’re trying to encourage here is not only things like number and counting, but some ‘intuitive’ facility with numbers and working with them.

Personally, I would avoid calculators for as long as possible. Everything should be head work, or head and paper work. One of the things I noticed with my degree level students was their almost pathological attachment to these devices. They could barely do the simplest calculations without reaching for the ‘security blanket’ of the calculator. It was wild, at times⁴. It was as if they didn’t trust their own heads.

Consequently, they had almost no real conception of ‘number’ appropriate for their level of education. If the calculator said it, it was true - and they had no inbuilt mechanism for figuring out whether the ‘answer’ they’d got actually made sense. I strongly suspect this over-reliance on calculators impacted their ability to learn algebra effectively - they were, in general, absolutely atrocious at it (again, at the appropriate level). I think by ‘contracting out’ their thinking to these little demonic devices they had never properly developed the right mental muscles (or had let those atrophy) so that their mental muscles were just horribly flabby.

An example of the kind of thing I would expect a student at this level to be able to do almost instantaneously would be to know that the answer to the multiplication of 39 and 51 is going to be around 2,000. I’d be OK with them using a calculator to get the exact answer, but I would not be OK if they’d mis-typed and didn’t realize that the calculator ‘answer’ of 20,000 was way out.

You can practice a bit more and get better still. Think of the multiplication in the following way

39 x 51 = (40 - 1) x (50 + 1) = 40x50 - 50 + 40 - 1

So you can readily see that the answer is going to be 11 short of the initial guess of 2,000. With a bit of practice it becomes easy to do this kind of thing in your head.

But here I’m presupposing a decent facility with number and their manipulations - which is something that only comes from practice and familiarity. There’s a reason why it’s important to rote-learn the times tables, for example.

If you never develop that kind of facility with number you’re not going to be able to think about them properly, or be able to use them properly (as a general rule). I suspect it’s the same with reading - if you never properly develop the fundamentals⁵ (like being able to work out what a word might be from the letters involved) you’re going to struggle more than you need to.

Playing With The Numbers

With young kids most of the ‘maths’ stuff and practice I’ve outlined here is really about getting familiar with arithmetic. But arithmetic is not really ‘maths’ - even though a lot of discussions about educational standards and the like seem to conflate the two.

Most of us, probably close to all of us, will need to be able to do some arithmetic in our lives. You’re earning a wage and you need to pay for stuff - so you need to partition that wage into pieces. But it’s not quite as simple as that. You need to think about the various costs and some might require an annual payment whilst some will be monthly or even quarterly. If you just look at your monthly outgoings and forget to save up for potential car maintenance you’re going to be a bit screwed when you need new brake discs or tyres. That’s just one example of where arithmetic and a little bit of mathematical thinking is required.

But how many of us will need to be able to solve a quadratic equation, or differentiate a function of the form f(x)g(x)?

One of the things that greatly angers me is the politicization of maths. Sure, it may be interesting to know that, actually, Ibrahim Al-Noodle-Doodle discovered a theorem before Lord Fortescue Smarty-Pants, but maths is a discipline that is both colour and culture blind. It is a universal thing that cares not one jot about your ethics or your feelings.

The fundamental theorem of arithmetic (FTA) is true whether it was first discovered by a white colonizer or a Muslim colonizer and it also has bugger all to do with ‘power structures’ or Oppression™.

I’ve picked on the FTA because it’s all about number. Or rather it’s about what we might call the counting numbers, or more technically, the integers. And it’s my view that number is where it all begins.

Let’s just suppose you’ve got good enough with your counting that you can count all the way up to 100. That’s just a list of numbers (integers). 1 cow in a field, 2 cows in a field, 3 cows in a field, . . . and so on. It’s not a fantastically interesting exercise.

Write them down (also not a fantastically interesting exercise). You could write them down in a line, or a grid, but in passing we note that order is important.

With a bit of effort, and maybe some visual aids like Mars Bars, you might realize that certain numbers⁶ can be ‘shared out’ equally between two people. There’s a pattern there lurking in this list. We call these numbers the even numbers and the ones that can’t be equally divided between two people we call the odd numbers. We might observe that all of the numbers on our list (remember we’re only talking about integers for the moment) come in two kinds; even or odd.

If you then go onto wonder whether this is going to still be true if we counted up to 200, or 1,000, or 10,000 then you’ve taken your first step towards mathematics (as opposed to mere ‘arithmetic’).

You try it out (it’s a really slow day and there’s nothing good on Netflix) and write out the first 1,000 numbers and notice the pattern holds. Your next thought might be to wonder about how you could convince someone that this pattern always holds, no matter how many numbers (integers) you write down?

Now you’re really getting into the swing of maths thinking, because you’re thinking how you might go about proving something.

We’ve started with one of the simplest things we could imagine; a list of numbers written down in order. But there’s a pattern lurking in there. It might not be a very interesting pattern, but it’s a pattern nevertheless. Your next thought might be to wonder whether there are any other patterns? You’re now in the realm of starting to do a bit of maths ‘research’.

You might also form a kind of ‘guess’ (a hypothesis) that might be something like the only numbers that can be divided equally (at all) are the even numbers. You work your way through the list and get to the number 9. You remember Alice, Bob, and Carol and recognize that if you gave them each three sweets, they’d have an equal share of the initial total of 9 sweets.

You’ve just disproved your initial conjecture, your hypothesis, by finding a counter-example.

You twig that perhaps you need to look at those numbers that can equally be divided between 3 people. You mark these on your list and you find another pattern.

But what about dividing between 4 people? You do that too - mark them on the list. You find that if you can divide a number equally between 4 people you can also divide that number equally between 2 people. There’s another pattern there; the 4-share numbers are all contained within the 2-share numbers (the even numbers).

Much of this seems ‘trivial’ and ‘obvious’ to us because we’re used to numbers through long practice.

You keep on doing this kind of thing and you build up more patterns. You notice that there are certain numbers that you can’t divide by any other (smaller) number into equal shares. You notice that all of these numbers are also odd numbers⁷ - but not all odd numbers are like this.

These special numbers, the non-share numbers, we call prime numbers.

You keep on doing this, seeing the patterns, and working out how numbers are related to one another and you notice another curious thing. Any number can be written down as a product of smaller numbers

6 = 2x3
9 = 3x3

And so on - and then you notice something really interesting.

There are numbers like this :

20 = 4x5 = 2x2x5
36 = 6x6 = 2x3x2x3 = (2x2) x (3x3)

You can break down every number into ‘atoms’ like this - except for those prime numbers which can only be written as something like 1x17 = 17, for example. When you’ve done this ‘atomic’ breakdown into smaller numbers you realise that all of those ‘atoms’ you’ve used are themselves prime numbers.

You formulate the hypothesis that any number (integer) can be ‘broken down’ into a product of these ‘atom’ numbers, the primes. So, for example, 315 = 3x3x5x7.

That’s the fundamental theorem of arithmetic.

We’ve started with what seemed to be a really boring thing, a list of numbers in order, and ended up spotting a really interesting pattern about the ‘structure’ of all counting numbers (the integers).

You have also realized that in this list, there’s a set of numbers, the primes, that act like elements do in Chemistry. They seem to be the ‘fundamental building blocks’ of number (integers).

You might, if you’re also philosophically inclined, wonder at this point whether this is something ‘discovered or ‘invented’. Was the pattern there, all along, just waiting to be discovered, or is it just some invention?

Your next job, of course, is to prove this hypothesis. You’re vaguely aware that there are even bigger numbers than 123,456,789 and you’re not going to be able to check them all (and besides which there’s a really interesting show that’s arriving on Netflix tomorrow).

These are the kinds of questions that get a mathematician’s juices flowing. Yet we’re all different. Some kids like playing with bricks, others like pulling the legs off spiders, not all are going to be fascinated with number patterns, or have any desire whatsoever to prove something about those patterns.

But, as a general rule, the more you can engage with the natural curiosity of your kids, the more success you’ll have getting them to be OK with numbers and their patterns. It certainly isn’t going to work for all, no matter how brilliant you might be at getting them interested in something.

Going On and On

One of the most curious things, and one of the most difficult to properly get your round, is the notion of infinity. Yet we ‘know’ about it even from quite early on. If there really isn’t anything on Netflix you want to watch until the weekend’s new episode drops you could keep yourself occupied by counting until it arrives.

Intuitively, you get the idea that this never stops. There’s no ‘end’ in sight and every time you might think you’ve got to the ‘end’ of counting you can add another number to the list.

If you’ve gone a bit further with your maths and are OK with the idea of division and fractions you could write down a related counting list :

1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, . . .

You’re still counting, though. You’re just putting your ‘count’ in the bottom of a fraction. You notice that the numbers get smaller as you go on (one half, for example, is bigger than one eighth). If Netflix really is a long way away you might get to a number like 1/10,000 and you realize it’s a whole lot smaller than 1/2.

You get the idea that as you keep going doing this counting and dividing you’re getting closer and closer to zero. With a bit more thought, and knowing the counting numbers have no ‘endpoint’, you can see that you’ll never get to zero with this process. You’ll get close, really close, (eventually) but you’ll always be able to go that one little bit closer (just use the next counting number on that list).

You see that for this division list you’ve created all of the new numbers (the results of the division) on that list lie between the values of 0 and 1⁸. But what about other numbers, say between 1/2 and 1/3? Can these always be written as a fraction like “counting number divided by counting number”?

This idea of making a list by counting turns out to be pretty important and interesting. In 1874 Georg Cantor showed that if you were to take all of the numbers between 0 and 1 (for example), there is no way to make a countable list of them⁹.

The ‘amount’ of numbers between 0 and 1 is ‘too big’ to be counted.

It’s a different kind of infinity than the one we got by counting; it’s ‘bigger’.

In fact, if we took any interval, say between 1/2 and 1/3 or between 1/1,000 and 1/1,001 or between 0.12345678 and 0.12345679, the numbers in that interval are too many to count.

Not surprisingly, this turned out to be a rather original and revolutionary idea.

Let’s circle back to those ‘non-share’ numbers, the primes again. You’ve made your list of counting numbers and you’ve marked off all the primes numbers. If you’d made a bigger list would you ever get to the point where you have ‘run out’ of primes numbers? Is there a number you could get to where you could say “That’s it. There are no more primes to be found?”

The answer is “No”. The set of primes is infinite - but it’s a countably infinite set. Just like the counting numbers themselves, the list of only prime numbers never stops; you’ll always be able to find a bigger prime than the last one you wrote down.

Is there a pattern? Well, sort of. There’s certainly some kind of ‘structure’ there because we know that all primes bigger than 2 and 3 can be written as either
6n + 1 or 6n - 1. This is a necessary condition, not a sufficient one. This means that there are lots of numbers of the form 6n + 1 or 6n - 1 that are not prime, but if you do happen to find a prime it will definitely be of this form.

17 (prime) : can be written as 6 x (3) - 1
80 (non prime) : can be written as 3 x (27) - 1

Now, here’s the thing. I’m writing this and thinking that being able to write any prime bigger than 2 or 3 as ‘6 times some number, plus or minus one’ is a really cool thing and fascinating. I’m going to guess that for most of you the response is a bit “meh!”

At the end of the day, all I can do is to explain what I find interesting, but not really why it’s interesting to me. I can hope to try to persuade you that, yes, it really is interesting, but you’re probably just going to respond with “So what? There are freaks out there who find Starmer to be interesting”.

And here’s the problem with trying to make maths ‘interesting’; it just isn’t going to work for everyone, and maybe not even most. Yet, as a strategy, trying to make maths as interesting as possible, in the classroom etc, is definitely the right thing to do - even though we know it’s not going to land with, probably, most.

As you get further into maths you find out that the prime numbers sort of pop up in your counting number list at seemingly random places. You can go ages without finding one and then, all of a sudden, like buses, two or three arrive in quick succession. They appear to be distributed amongst all counting numbers quite randomly. Is it actually random¹⁰?

Dunno. Nobody knows. Perhaps the greatest unsolved problem in maths is the Riemann Hypothesis which is about prime numbers (although that’s not immediately obvious from the usual statement of the hypothesis). If this turns out to be true then we’ll be able to say that the primes are distributed ‘randomly’ (and if this hypothesis is true lots of other interesting things besides this will also be true). If we go by the efforts of some mathematicians who have checked the hypothesis up to some incredibly high value (computationally) and found it to be true - so far. We can’t be sure that if we go further and further along the number list we won’t get to a counter-example. There is not, as yet, a proof that the Riemann Hypothesis is actually true.

All of this stuff from the list of counting numbers.

That’s where we started. We just counted things.

We came, we saw, we counted¹¹.

Conclusions

Not many, except that learning maths is hard work, and you can make that hard work seem more enjoyable (or worthwhile) by making maths as interesting as possible, but that isn’t going to work for everyone (probably most). Not the world’s greatest insight, to be sure. But it’s just the reality - it’s symbolic of our struggle against symbols.

1. This may, of course, be more of a reflection on my own failings. Like any other human endeavour there seem to be ‘naturals’ who have a gift and I’ve seen quite a few such lecturers. They would probably have a lot more success than me in getting across the excitement and relevance

2. That number i appears explicitly in the Schrödinger equation which, we believe, describes ‘reality’ at the quantum level. It’s not something you can get ‘rid of’. Reality at this level, it seems, is profoundly dependent on complex algebra

3. You might end up with no teeth and diabetes, but it’s worth it to produce the next Gauss, surely?

4. Whilst invigilating (proctoring) a Master’s level exam in advanced maths techniques I witnessed one student type “1 x 7 =” into their calculator. I think that was the wildest example I saw, but there were plenty of others

5. I have read that one popular technique for ‘teaching’ reading these days is to get the student to remember a word ‘pattern’ without ever properly spelling it out. This strikes me as effectively disabling a student - and I think you need a bit of both; the ‘trad’ way and the ‘pattern recognition’ thing. But whichever methods get used, the key component is practice

6. I’m going to stay with the integers here (the counting numbers) so fractions are not allowed, for the moment

7. Apart from the number 2, which is also considered to be prime

8. We’re making this list by using the counting numbers, but the results we get from the division (e.g. 1/2 = 0.5) are no longer counting numbers.

9. Technically what this means is that there is not a one-to-one correspondence between the counting numbers and the numbers between 0 and 1. If you think about this a bit more then you realize that it means that not all of the numbers between an interval can be written as a fraction of ‘counting number over counting number’. In another spectacular bunglement of terminology we call these non-fraction numbers the irrational numbers

10. Technically we’d have to say ‘pseudorandom’, but let’s skirt over that

11. Venimus, vidimus, numeravimus is the Latin version that Google’s AI gives me