Bells and Whistles

I feel like taking a break from the usual woke, gender, and censorship headaches. It’s time to get technical again.

I want to talk about one of the most extraordinary pieces of physics of the 20th century. It has profoundly altered our view on things. We can credit Einstein, together with his co-authors Podolsky and Rosen, with getting this particular quantum ball rolling. They proposed a very simple (thought) experiment which, they claimed, showed that quantum mechanics (QM) was incomplete; that there must be some hidden features (or variables) underneath everything.

They were wrong, but with typical Einsteinian insight they went right to the heart of the problem. It’s one of those instances where some truly brilliant scientist gets something wrong, but for really interesting reasons.

I’m talking about the notion of quantum entanglement.

You’ve probably heard about this, if not in pop science books, in science fiction shows, at least. It’s important because of the possibility of generating new technology from this phenomenon, but it also seems to say something very fundamental about ‘reality’. If the universe is quantum, then it’s very strange indeed.

The original paper of Einstein, Podolsky and Rosen was published in 1935. It is known simply as the EPR paper. But it wasn’t until nearly three decades later, in 1964, were we able to properly get to the heart of the matter as to why the EPR paper was wrong. In that year, the great Northern Irish physicist John Stewart Bell¹ (pictured below) published one of the most important physics papers ever written.

Today I want to talk about what’s in that 1964 paper.

Bell’s paper was called On The Einstein-Podolsky-Rosen Paradox. Doesn’t really sound like something that’s going to set the world on fire, does it?

Bell’s analysis was remarkably general, relatively simple, and did not require any quantum mechanics whatsoever. Although it’s one of the most important results in QM, his result did not use QM at all.

That sounds like a bit of a paradox in itself, but let’s see what he did.

Alice and Bob Get Bored in London and Berlin

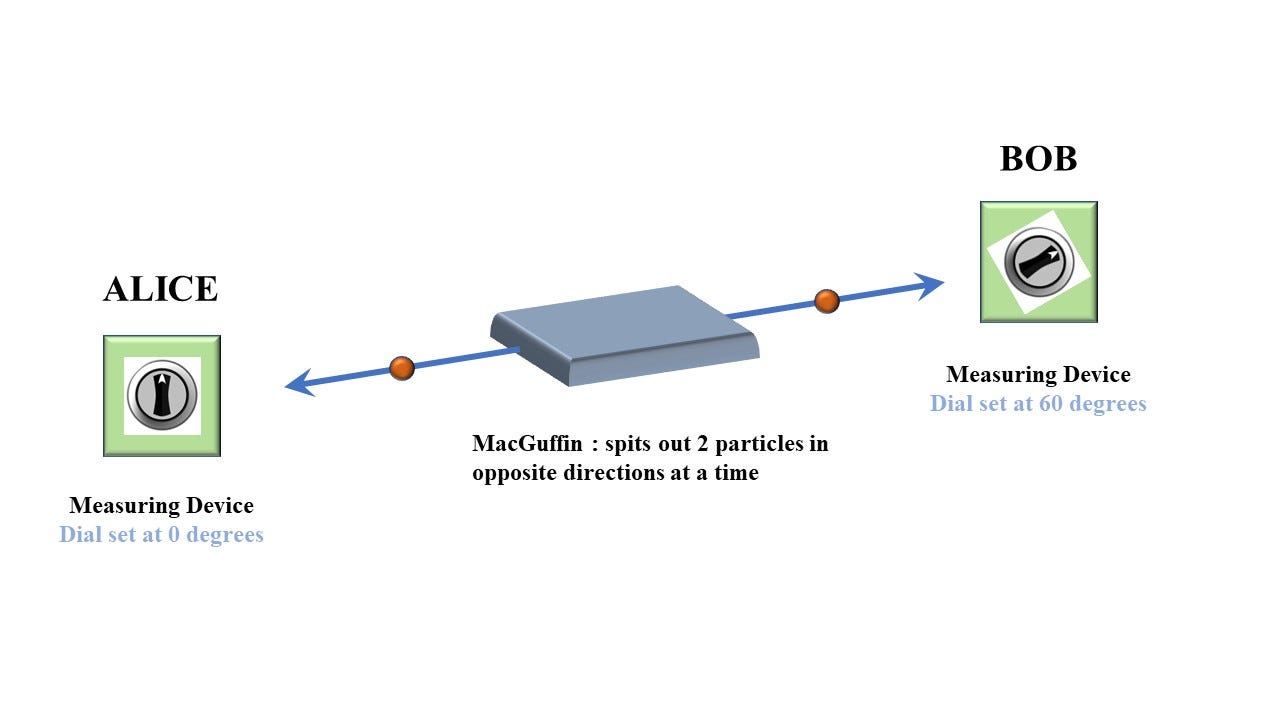
We start off with a very simple experimental system. Let’s not worry, for now, about whether such a system actually exists (it does), but let’s just play with the idea and see where we go. Here’s a picture of what Bell had in mind

So, what do we have here?

• We have some kind of black box, a MacGuffin, which spits out a pair of objects (particles) in opposite directions. We imagine we can set our MacGuffin to produce these particle pairs at a certain rate (so, maybe, 1 particle pair every minute, for example).

• We have Alice and Bob, our intrepid experimentalists, who are going to measure some property of these particles. Alice and Bob (and their laboratories) are assumed to be some distance from one another. We might, for example, imagine Alice to be on Venus and Bob on Mars. But, more realistically, we might suppose Alice to be in London and Bob to be in Berlin, for example.

• Alice and Bob each possess an identical measuring device. The device has a dial that can be set at 3 positions; 0°, 60°, and 120° (3 different angles). Alice and Bob are free to choose which of these settings to pick. We’ll refer to them as setting A, B and C, respectively.

And that’s it.

Almost. There’s just one other thing that we need to be aware of. The measuring devices of Alice and Bob spit out a binary result. We can call this a ‘yes’ or a ‘no’, or a 1 or a 0, or a +1 and a -1. Doesn’t matter. For each setting we get one of two possible results.

We break everything down into timeslots; minute 1, minute 2, minute 3, and so on. The results are recorded. So we end up with a kind of list.

Timeslot 1 : Alice setting, Alice result, Bob setting, Bob result
Timeslot 2 : Alice setting, Alice result, Bob setting, Bob result
Timeslot 3 : Alice setting, Alice result, Bob setting, Bob result
Timeslot 4 : Alice setting, Alice result, Bob setting, Bob result

and so on . . .

Alice and Bob are nothing if not dedicated, and they repeat these experiments for many, many, thousands of timeslots. In each timeslot they randomly select the setting of the measuring device. Let’s see now, particle 1,004,781 is on its way to me, which setting A, B or C should I pick for this one?

Alice doesn’t communicate with Bob. Indeed, she only hopes that Bob is at the other end and dutifully keeping up his end of the experimental bargain.

It’s only afterwards when she and Bob meet for croissant and chocolat chaud in Paris do they get to compare their respective results.

Alice : look here, Bob, I don’t know why they asked us to do this experiment. All I’m getting is total randomness. Every which way I split the data, it’s all just random. I look at the results for setting A; random. The results for setting B; random. Group together the results for A and C; random. I’ve run every statistical test I can think of - and they pass the criterion for randomness better than any dataset I’ve ever seen before

Bob : Me too. It’s all just a bunch of random stuff. Why did we spend the last 3 decades collecting this data?

And here we pause because there’s something important to point out. They have a dataset. It’s just a list of numbers; a table. There’s nothing magical or special about it is there?

The magic happens when Alice and Bob dig a little deeper and directly compare their results.

Bob : Hey, Alice. I’ve just noticed something odd. Every time you set your device to A and I set my device to A we got the same number².

Alice : What? Let’s see. You’re right. And if we look at the B results - you picked B and I picked B, we got the same number too!

Bob : (getting excited now) And there’s something else. Look at when you measure A and I measure B. We got a partial correlation. It’s not just pure randomness!

Alice : What on earth was that MacGuffin generating?

This is very much the point. What IS this black box, this MacGuffin, doing? What can we say about the black box from analysing the data we have collected?

Well, we have correlated data. There must, surely, be some reason why the data is correlated in this fashion (perfect correlation when the same settings are chosen, partial correlation when different settings are chosen)?

If there exists this correlation (both full and partial) then there must be some internal property (or set of properties) of the particles that generate this correlation that is seen in the results. Right?

That certainly seems to be correct doesn’t it?

And here we’re getting our first inkling of what the relevance of this experiment has for QM. We’re forced, by the results, into making some (extremely reasonable, one might say obvious) assumption about the particles produced by the black box. There’s something hidden, something underneath, causing this correlation.

The Technical Bits

Time to pin this down.

We start off with two very reasonable assumptions, one of which we’ve already stated

1. There is some property (or set of properties) that exists, independent of measurement, possessed by the particles that generate the observed correlations

2. No signal or influence is transmitted between Alice and Bob, or the particles, that can affect the results (or the choice of settings) that travels faster than light.

The second of these assumptions seems very reasonable too; why should the choice of setting of Alice be able to influence the result Bob gets? Theoretically, one supposes, we could have some clever signalling mechanism between the two measuring devices that correlates the results, but we know that any such signal can’t get from one device to another faster than light can.

The first is usually given the terminology of the assumption of realism and the second is usually given the terminology of the assumption of locality. They often get lumped together as one, so we have the assumption of local realism.

Unfortunately, we’re dealing with results that are statistical in nature. A partial correlation means that we get agreement more often than we would expect from purely random data. But there’s no way of predicting which particular result will show agreement and which won’t. So we need to use the tools of analysing uncertainty. Which means we’re going to have to talk about probabilities.

If we’ve got many thousands of results we can form really good estimates of the probabilities involved.

We can look at the data and use it answer questions like; what is the probability that, for a given timeslot, Alice gets the result 1 when choosing setting A and Bob gets the result 1 when choosing setting B?

Working out what this probability is is a simple matter of counting. We can “read it off” from the data.

In more formal maths terms we’d write this probability question something like this

\(P(A=1,B=1) = \space ?\)

So you can see that from the data we’ll be able to construct good estimates for the various probability distributions

\(P(A,B), P(A,C), P(B,A), P(B,C), P(C,A) \space \mbox{and} \space P(C,B)\)

It’s true that we can form these probability distributions.

But we’ve already stated that there must be some hidden properties driving all of this. Or we’ve assumed there must be. So really what we have here are conditional probabilities. The results we get are conditional upon these hidden properties. We can get to the unconditioned probabilities (like P(A,C), for example) by ‘summing up’ over all of these internal, hidden, properties. That’s what we’re constructing from the data when we form³ things like P(A,C) - the effect of ‘summing up’ over all of these internal properties.

The formal structure in probability terms looks like this

\(P(B) = \mbox{ sum over all possibilities for A of} \space P(B|A)\)

We can think of this as a kind of ‘averaging out’ of the effect of all of the influences of A. This vertical bar thing is read as ‘given’. So the expression P(B|A) would read the probability of B (having a certain value) given that A has this particular value.

An example might be, what is the probability my plants die given that the temperature is 1 degree below zero?

If you want to know the overall probability that your plants die in a year, you’d take the conditional probabilities and sum up over all of the temperatures (assuming temperature is the only relevant variable here).

So, Bell argued, that if we’re going to run with our assumption of realism then what we really have is a conditional probability that we can formally write as

\(P(A,B| \lambda)\)

The lambda here is the usual symbol that stands for these ‘hidden’ properties. It could be one property, it could be many, the actual specific number or form doesn’t matter. When we form our probabilities like P(A,C) from the data, we’re really just summing up over this conditional probability with the lambda thing in there.

For Whom The Bell Tolls

Using these conditional probabilities - recall that these conditional probabilities are the way of including our assumption about realism - Bell was able to prove, fairly straightforwardly, that the probability distributions we can generate from the data must satisfy the following property that is known as Bell’s Inequality

\(| \space P(A,B) - P(A,C) \space | \leq 1 + P(B,C)\)

It’s very important to note that this is based on entirely classical reasoning about probabilities together with the very reasonable assumption of local realism. There’s no quantum mechanics anywhere in this set-up, or the derivation.

It’s also interesting to note that George Boole, over a century earlier than Bell, derived a very similar kind of inequality when analysing the properties of joint probability distributions P(A,B,C) where A, B and C represent binary variables.

Don’t get too hung up on the specific form of that inequality equation above. In certain respects, the actual form of it is irrelevant. What is important, though, is that it’s a relationship that must be satisfied by any theory of the MacGuffin and the particles it produces that uses the assumption of local realism.

Whatever the theory is, if it’s based on the assumptions of locality and/or realism, then the probability distributions we derive from it have to satisfy this relationship.

Lovely jubbly. You see what we have here now, don’t you? We can run this experiment in real life, just count things up from the observed data, and see if the probabilities we get are constrained by this relationship.

If they are, then whatever the particles are, whatever the MacGuffin is doing, we know we can construct some locally realistic theory to explain it.

The converse is more disturbing and is really what Bell’s theorem is all about.

If there exists in nature a system like this, a real experiment we can do, AND we find that this relationship between the probabilities does not hold when we analyse the data then, whatever we have, it cannot be described by any locally realistic theory of nature.

Sure enough, there’s a quantum mechanical prediction that such systems exist in nature and so we arrive at Bell’s famous theorem.

A locally realistic theory cannot reproduce all of the results of quantum mechanics.

And also sure enough, we can do these kinds of experiments. The 2022 Nobel prize in physics was awarded to Alain Aspect, Anton Zeilinger and John Clauser for “experiments with entangled photons, establishing the violation of Bell inequalities . . .”

The Campness of Campanology

You may recall that some time ago I wrote a piece about a physicist who claimed that QM demonstrated that the universe is “queer”. Because I have a fetish for stupid titles I can no longer remember what I called that piece. Sorry about that.

It’s really the “queerness” (which is just synonymous with strangeness in context here) of results like Bell’s Theorem that this physicist was referring to here. She drew a parallel between that and sexual deviance⁴ where no such parallel exists, of course. But such is woke and their delusions.

And Bell’s Theorem really does point to a deep strangeness at the heart of this thing we perceive as “reality”.

What it’s saying is that if we assume things possess properties independent of measurement, real intrinsic properties, then any theory based upon this assumption will not be able to explain everything we see in nature.

Either that or we must admit the possibility that there are influences that act instantaneously across vast distances.

Or both of these things.

Such things exist. The experiments have been done. The most fundamental description of our perceived ‘reality’ cannot be one involving locally realistic variables. Which is equivalent to saying that such properties, such variables, do not exist in nature.

Our world then, at some fundamental level, rests on ‘stuff’ that doesn’t have actual concrete properties in and of itself - it has potential properties which are manifest upon measurement.

We’re not hearing Bells and Whistles, just the possibility of them.

1. I promise not to mention that Bell is (a) male, (b) white and (c) dead. I mean, come on Man, what have dead white men ever done for us, eh?

2. In the original analysis the results were anti-correlated. If both Bob and Alice had set their devices to measure A then if Alice measured a +1, Bob would see a -1. Calling it an anti-correlation is just too darned confusing and silly though. An “anti” correlation is still a correlation. The actual numbers, whether it’s 1 and 0, or +1 and -1, that are obtained is also irrelevant.

3. This really is just done by counting. You look at the results where Alice measured A and Bob measured B, for example, and just count agreements and disagreements. The probability is the number of agreements divided by the total number of experiments done where Alice chose A and Bob chose B. Or you can fine-grain a bit more and count the number of specific agreements (Bob gets 1 and Alice gets 1, or Bob gets 0 and Alice gets 0)

4. “Deviance” is meant in its strictly technical sense of departing from the norm, here.