I have to say, my brain is slowly turning to some gloopy mess after trying to navigate a week’s worth of “news” and opinion. Not to mention my spirit. There was a time when the world seemed to make some sort of sense to me.
I think one of the reasons I have focused on gender ideology over the past months is not so much that it is important (which it obviously is) but that it is an example of something that is stark raving bonkers. How did we ever manage to talk ourselves into the position that in order to become, one merely has to identify? And that’s only one of the deranged dogmas that have been voided from the bowels of the all-consuming gender ideology behemoth.
Compassion and kindness is one thing, living in some weird sexualised (and genderised) fantasy world that bears only a superficial resemblance to reality, quite another.
But nutters have always been with us. What’s interesting about the gender ideology stuff is how many ordinary non-nutty people seem to have swallowed it.
Today I want to try to simmer down a bit and get a bit technical. I feel like I need some kind of anchoring in sanity and rationality before attempting to sally forth onto the hellish woke battlefield once again.
This morning I’ve seen a couple of tweets stating things like “half of my 14-year-old granddaughter’s class identify as trans”, or that “half of my daughter’s class are LGBTQ+”
My immediate thought, beyond social contagion, is what’s the probability of that?
Probability is a fundamental part of our lives and a fundamental part of how we view the world. We’re conditioned to think in terms of risk, for example. The risk of nuclear war, the risk of climate change, the risk of covid, the risk of not vaccinating or wearing a mask, the risk of suicide if gender-affirming care is not available, and so on.
Everywhere, we’re invited to frame things in terms of risk. Warning; there be dragons ahead.
What we’re all pretty hopeless at, unless we put in some effort, is putting this risk landscape into perspective. It’s hard not to be swayed by a headline that says “eating bacon doubles your risk of a heart attack”. Eating bacon becomes a risky business - at least in our minds. Our subconscious will have got the message; bacon = bad.
Evolution has tried to give us a balance somewhere in between being paralyzed by fear and being wholly unconcerned with risk at all. Neither of these extremes would have been a great survival strategy. But, alas, it has also left us vulnerable to manipulation and this has been exploited by politicians and tyrants throughout history. Just two examples; Hitler stoked up fear of the Jews, Trudeau stoked up fear of the unvaccinated. There’s no essential difference in technique here. Both leaders, presumably, thought their highlighting of the ‘risk’ was appropriate and justified in some way.
So, how do we combat the current pandemic of (alleged) risk that seems to be plaguing us?
The only real way out of this is by education. To be more specific, it’s a particular kind of education. It’s the kind of education (and it could be self-education) that questions, and attempts to place everything within a rational framework. It’s a kind of day-to-day working out of the scientific method applied more generally which I state in typically Riggerian fashion
If something doesn’t fit, your ideas might be shit
Being cynical and wrapping the bacofoil round my head (it protects against both mind control and those dangerous elementary particles known as bacons) one might suggest that the modern attack on The Enlightenment and its values is part and parcel of preventing this kind of education from occurring. Those colonialist and dead white men just can’t be trusted, don’t you know?
One of the things we can do is to educate ourselves, and others, about probability. We make probability assessments all the time. It’s a bit cloudy today, should I wear my raincoat? We read the morning paper and it tells us that the risk of a catastrophic weather event is increasing. Should we be worried? We need some basic notion of probability in order to navigate our lives. We need to ‘do’ probability every day. But we are, by and large, bloody awful at doing it rationally and correctly.
One of the devices that helped me, and hopefully my students, was to cast certain probability questions in terms of what is known as a binary communication channel. I’ve found it to be a really useful way of cutting through the bullshit and confusion.
The idea behind such a channel is that you have sender who is sending some message encoded in binary. It might look something like this:
message sent : 11100010100110
At the other end the receiver gets a ‘message’ which might look like this:
message received : 11101010100010
There is a difference between the sent and received messages here. The channel has introduced some errors. The job of the receiver is to try to figure out what message was actually sent, given the message that was received.
One question might be “why do we need probability at all here?”. After all, the sender is not just typing random shit, but sending a definite well-specified message. We use probability to help us analyse situations where there is uncertainty. It doesn’t matter where that uncertainty arises. In the case of a communication channel there is uncertainty about the message - even though the user is sending a definite message, the receiver only knows that any message might have been sent (where “any” here means any possible message given the constraints. Obviously, if the sender has sent 101 as a message, he hasn’t sent you the first chapter of War and Peace).
So, if the sender has sent 101, the receiver knows that there are 8 possible messages that could have been sent; 000, 001, 011, 111, 100, 110, 101, 010.
We use probability to help us understand the uncertainty of the receiver.
On a perfect channel there are no sources of error and so what gets sent gets received. But what if there’s a source of ‘noise’? What if, sometimes, a 1 gets changed into a 0 along the way?
We use the idea of a conditional probability to get a handle on this. We ask: what’s the probability that the ‘1’ I sent gets mangled and turned into a ‘0’? Normally we use the word ‘given’ to indicate this and so this gets written as: the probability that a ‘0’ was received given that a ‘1’ was transmitted.
As always in technical subjects, although we could write out big long sentences all the time, we want to be able to condense things and so we use symbols to do the heavy-lifting. Here we would write P( a ‘0’ is received | a ‘1’ was sent). We might even want to condense it further into P(0|1) - although this can sometimes be a bit risky. The vertical line here is just a convenient way of indicating the word ‘given’.
Once we’ve overcome our fear of symbols and realized that they actually help us we can begin to use them to really get to the nitty-gritty. It does take a while to become comfortable with this condensed, symbolic approach, but it is really useful.
Now we can think about ‘errors’ and how to characterize them. If a ‘1’ was sent, but a ‘0’ was received, there has been an error on the channel. We can use this approach to think about testing for a disease. If you ‘receive’ a 0, which is a negative test result, but you actually have the disease (i.e. you ‘sent’ a ‘1’) then the ‘channel’ (the test procedure) has introduced an error. In this case, in the context of a medical test, we’d call it a false negative.
In our condensed, symbolic format this is just P(0|1).
This switch of perspective to a communication channel can help us understand some of the issues with medical false positives, for example.
Suppose we had a disease prevalence of 0.1% which is 1 in a thousand. This is like someone sending a message where only 1 in a thousand of the symbols that are being sent is a ‘1’. Now suppose the channel (the test) has an error rate of 10%. It turns 10% of the ‘0’ symbols into a ‘1’. The receiver is going to get a message that is made up of about 10% 1’s, on average. But we know that only 0.1% of the originally transmitted symbols were actually 1’s. The conclusion is that most of the received 1’s are, therefore, arising from errors. Which means that those people who received a ‘1’ are probably not infected at all, in the context of medical testing.
I can’t speak for you guys, but, for me, the impact of disease prevalence on the results of medical tests becomes much clearer when re-casting the problem in terms of a communication channel.
So, what about ‘social’ issues?
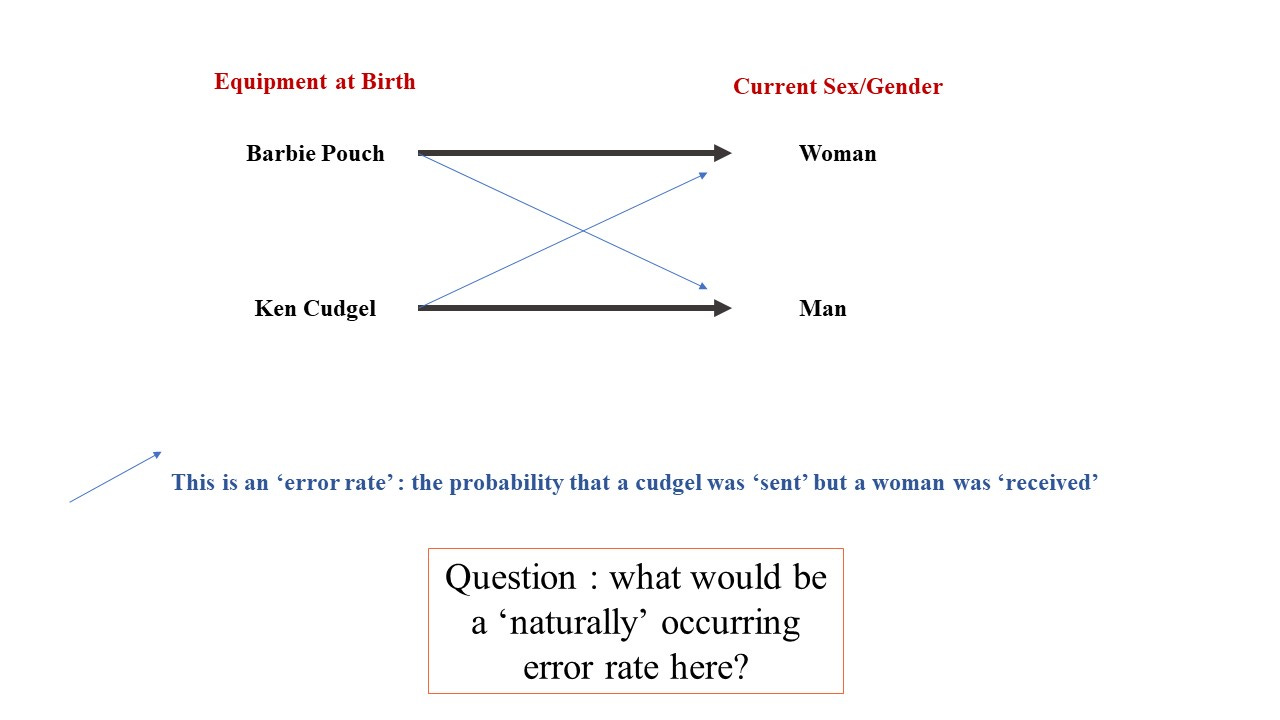
Let’s think about that earlier tweet which claimed a 50% ‘trans’ rate in a particular class. Let’s cast this as a communication channel. Here’s what it would look like:
So, on the left we have the ‘sender’ and the message is binary; pouch or cudgel? On the right we have the ‘receiver’ which is, some time later, being asked to disentangle the message that was ‘sent’.
We can see that those born with cudgels who now think of themselves as women represent, in the context of a communication channel, an error on the channel. If the 50% trans rate is true, or even remotely typical, we can see that something has changed that is causing a huge rise in the number of errors on the channel.
A more pertinent question might be flippantly asked: how many lions wear nail polish?
Has the human race really evolved to the point that our biology gets it wrong 50% of the time?



Assessing risk used to be something every child learned to do in everyday play and interactions. You know, before being young, active and a bit wild became a verboten part of childhood.
Boy 1: I want to climb that big tree.
Boy 2: I climbed it last month, fell out and broke my arm.
Boy 1: Hmm, I still want to climb that tree. Assesses risk and decides to climb, falls and breaks his arm. Lesson in risk taking learned.
A week later...
Girl 1: I want to climb that tree.
Boy 1: (with lovely blue casted arm) “Go for it”!
Assessing risk is a learned trait that todays children are being deprived of developing. Same as learning coping sills and critical thinking. We’ve devolved into a world of perpetual adolescence.
“Identify” = Play pretend. You know, like five year olds do- put on Mommy’s dress, now you’re Mommy…