I'm going to talk some balls

Apologies for the more infrequent posts this last week or so. I’ve been cogitating. And my cogits don’t run as fast as they used to.

I’ve been trying to come up with simple ways of demonstrating my concern over what I can only view as a mis-categorization, or mis-classification, of deaths after being Goo’ed. My view is that this is a potentially very serious problem indeed. In order to show this I’m going to have to dip a little toe into the potentially problematic pool of probability.

One of the problems is that probability stuff can be difficult. Although the math is often quite straightforward (algebraically speaking), the concepts and understanding are, for most, not at all straightforward (and I’m including myself in this ‘most’). Probability is one of the damndest things to get right. It’s one of the reasons so many people make a total bollox of interpreting statistics - fundamentally it’s an error of probability.

The Monty Hall Problem

There’s a very famous example which illustrates the kind of difficulty we face with probability - it’s known as the “Monty Hall Problem”.

You’re on a game show and in front of you are 3 boxes (in the original there were doors). One of those boxes contains a diamond. The other 2 are empty. You are asked by the game show host to choose one box. After you’ve chosen, the host puts your choice to one side and from the remaining 2 boxes he removes one which definitely does not have the diamond (he knows which box contains the diamond).

There are now 2 boxes left. One of these boxes contains the diamond. The game show host now asks you whether you want to change your mind and choose the other box, the one you didn’t originally pick. Should you change your mind?

At this point most people think there are 2 boxes left so it’s a 50:50 choice and so there’s no point changing your mind. They are, however, wrong. You really should change your mind - the diamond is twice as likely to be found under the box you didn’t pick than the one you did.

It is comforting to know that even spectacularly brilliant mathematicians can get this wrong.

The reasoning is simple - once you see it. It’s seeing it that is difficult. Frame the question differently. Suppose you had 100 boxes to choose from. You make a choice and your choice is taken away to another room. What is the chance that the diamond is in this other room? It’s 1 out of a hundred.

There are 99 boxes remaining in front of you and the diamond is 99/100 likely to be in one of them. Now the host removes 98 that don’t have the diamond so that there is just one box left in front of you. Should you change your mind and pick this one? Of course you should - there is only 1/100 chance your initial pick was correct, so even though there are now only 2 boxes to pick from, you know the diamond is 99% likely to be here in this room with you and not in the other room.

Exactly the same reasoning applies when you have only 3 boxes.

There are lots of other ways to get your knickers in a twist with probabilities.

Rates not raw numbers

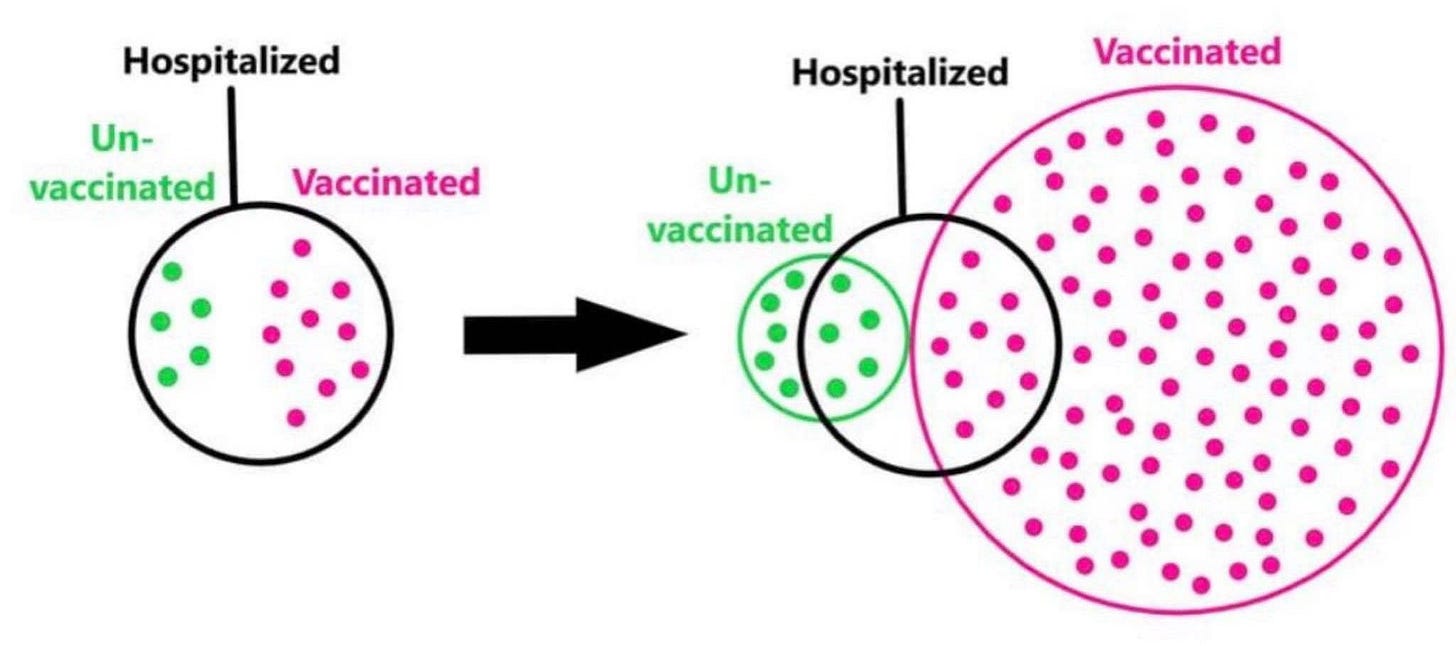
Suppose you see a stat like there were 500 deaths (from covid) in the vaccinated and only 100 deaths (from covid) in the unvaccinated. Many people would immediately think this stat proves the vaccine is not effective. Unfortunately, this is not so. This graphic explains things beautifully, although it’s referring to hospitalizations and not deaths.

You can see that by just focusing on the small piece that is the black circle you get a misleading picture. This is why it’s important to focus on rates, rather than raw numbers. But rates are, essentially, probabilities - or at least a reasonable approximation to probabilities when large enough numbers are involved.

Just looking at the small piece, the black circle, is an example of what might be called a ‘base rate fallacy’.

A load of balls

In order to see what’s going on, and what the potential problems are, I’m going to cast everything in terms of balls in bags. Yes, it’s mundane - but it removes us from the more emotive language of deaths and vaccines.

We’re going to imagine red balls and blue balls in a bag. Furthermore, we’re going to assume that some of these balls will have a spot. One question you might ask is the following:

If I put my hand in the bag and pick out a ball at random what is the probability that the ball I pick will be red AND have a spot?

You can ask other questions too. For example:

If I put my hand in the bag and pick out a ball at random what is the probability that the ball I pick will have a spot?

In the first case you’re interested in both the spot and the colour (technically this is known as a joint probability). In the second case you’re only interested in the spot, independent of colour.

We don’t want to keep having to write out all that verbiage all the time, and so we adopt a mathematical notation that shortens things - but it’s really just a shorthand way of writing down the verbiage. So we might write c as the colour variable which can have the values c = B or c = R (for blue and red), and we might write s as the spot variable which can have the values s = 1 and s = 0, where zero represents ‘no spot’.

So our first question above boils down to the shorthand representation

P(c = R, s = 1) = ?

which we read as “the probability that the colour is red AND there is a spot”. The comma in the equation here means ‘AND’. You can see why the shorthand is necessary - although it does look a bit more scary than the word version.

There is another way to slice the probability cake - and this is where the potential for lots of confusion really begins to creep in. Let’s suppose we take our original bag with its mix of red and blue balls and we now put all the red balls in one bag and all the blue balls in another bag.

Now, when we pick out a ball from the red bag we know it’s going to be red - for sure. So what’s the probability of picking out one with a spot?

This is what’s known as a conditional probability - and this would have the shorthand P(s | c) where the vertical line here is read as “given”. So we might write:

P(s = 1 | c = R)

which gets read as the probability that we pick a ball with a spot given that we are only picking from the red balls

I hope by now you can see that the math notation really does allow us to compress a whole load of verbiage into a neater expression.

Running some numbers

The expressions, as neat as they are, do get a bit awkward to keep track of - it takes a fair bit of practice to get comfortable with them. It’s usually helpful to have a concrete example with numbers to fall back on.

So, we’re going to imagine we have 1,000 red balls such that 100 have a spot. We will imagine 10,000 blue balls such that 500 have a spot. Schematically this looks something like this

Now if we had just the one bag, with all the red and blue balls in it, and we reached in and picked out a ball at random we’d be 5 times more likely to pick out a blue ball with a spot than a red ball with a spot.

If we now made the statement “you’re more likely to have a spot if you’re blue” we would be wholly incorrect. This would be a ‘base rate fallacy’ and comes about because you’re comparing joint probabilities rather than conditional probabilities. This is the same problem as saying “you’re more likely to die from covid if you’ve been vaccinated” from the raw numbers above.

In order to work out things correctly we actually need the conditional probabilities. We need to separate red from blue and ask:

What’s the probability of picking a spotted ball from the red bag compared to the probability of picking a spotted ball from the blue bag?

In this case you have a 1/10 chance of picking a spotted ball from the red bag (100 chances out of 1,000 total) whereas you have only a 1/20 chance of picking out a spotted ball from the blue bag (500 chances out of 10,000 total). So you’re twice as likely to have a spot if you are red than if you are blue.

Spotted blue balls are rarer than spotted red balls, in their own respective populations.

So far, so good, for Team Goo.

We’ve avoided the ‘base rate fallacy’.

If we just left things here, drawing this simple analogy between the colour of our balls and covid vaccinations, we’d be singing the praises of the Goo. There are several problems, however. There are plenty of what are technically called confounders when we consider the more complex picture afforded by covid. This is just a fancy way of saying there are other potential factors at play - that just using the single variable of Goo status may not give the most accurate picture.

Really what we’re asking is are the two populations (jabbed and un-jabbed) the same in every other respect except for jab status?

If they are - then we’re OK as it stands (provided we haven’t made some other error like mis-classification). But if they’re not, these things have to be accounted for. I’m going to leave this question, the question of bias, for another day. What I want to look at (again) is the problem of mis-categorization, or mis-classification.

And don’t it make my red balls blue

So we’re going to change things up a little. Let’s imagine we start with 11,000 red balls such that some of them will develop a spot if left untreated. We’re going to treat 10,000 of these balls with some process that is supposed to help with the spots but it also turns them blue after 2 weeks.

We’re also going to adopt the weird rule that if a treated ball develops a spot during the 2 week period before it turns blue it will be classed as a red spot ball.

We’re now going to wait a further 4 weeks to see how our blue balls fare - do they develop proportionally fewer spots?

Let’s suppose there are 50 treated balls that develop a spot during this 2 week period after treatment and 50 untreated red balls also develop a spot during the entire 6 week period. In the 4 week period after the end of the 2 weeks we find that 500 of the blue balls develop spots.

Every single one of the 10,000 treated balls go through this 2 week period and so the probability of spotting during this period, when treated, is 50/10,000 = 0.005. This is 10 times lower than the spotting probability for untreated balls during the 6 week period, and nearly 10 times lower than the spotting probability for 4 weeks after treatment.

When this 6 week period is up here’s what we would have

• 1,000 untreated balls (still red)

• 50 untreated (red) balls with spots

• plus 50 (treated) blue spot balls considered to be “red”

• 9,050 blue balls, 500 with spots

How effective has our treatment been?

If we just look at the conditional probabilities appropriate to this mis-classification scheme we have (to 4 decimal places) :

P(spot | colour is “red”) = 100/1050 = 0.0952

P(spot | colour is “blue”) = 500/9,050 = 0.0552

So, based on this calculation, you would say you are 1.7 times more likely to have developed a spot if you’re a red ball. Our treatment works, you say, and you proudly trot off to every media establishment to trumpet your finding.

The legerdemain here is that really we should be looking at treated vs untreated, and not the colour. Here the relevant conditional probabilities are

P(spot | untreated) = 50/1,000 = 0.05

P(spot | treated) = 550/10,000 = 0.055

This is not a quote, but I don’t know how else to highlight the important conclusion here

So, you are actually more likely to develop a spot, if treated, than if left untreated. If you allow the legerdemain of mis-classification your result says the opposite!

You’ve turned something with negative efficacy into something with nearly a 50% (apparent) efficacy merely by buggering up the categories.

Summary

What this example shows is that just by the single expedient of mis-classification we can drastically change the interpretation of whether a treatment has been effective or not. This is without considering any other potential biases that might exist - which might not be the case for balls, but is certainly the case when we apply the same naïve reasoning to covid deaths.

The ‘base rate fallacy’ is certainly a real potential pitfall that we must avoid, but it is far from being the only pitfall we need to avoid when interpreting covid stats.

---